Inicio de la Mecánica Cuántica: De la catástrofe ultravioleta a una revolución discreta

Un Problema Inesperado 🚨

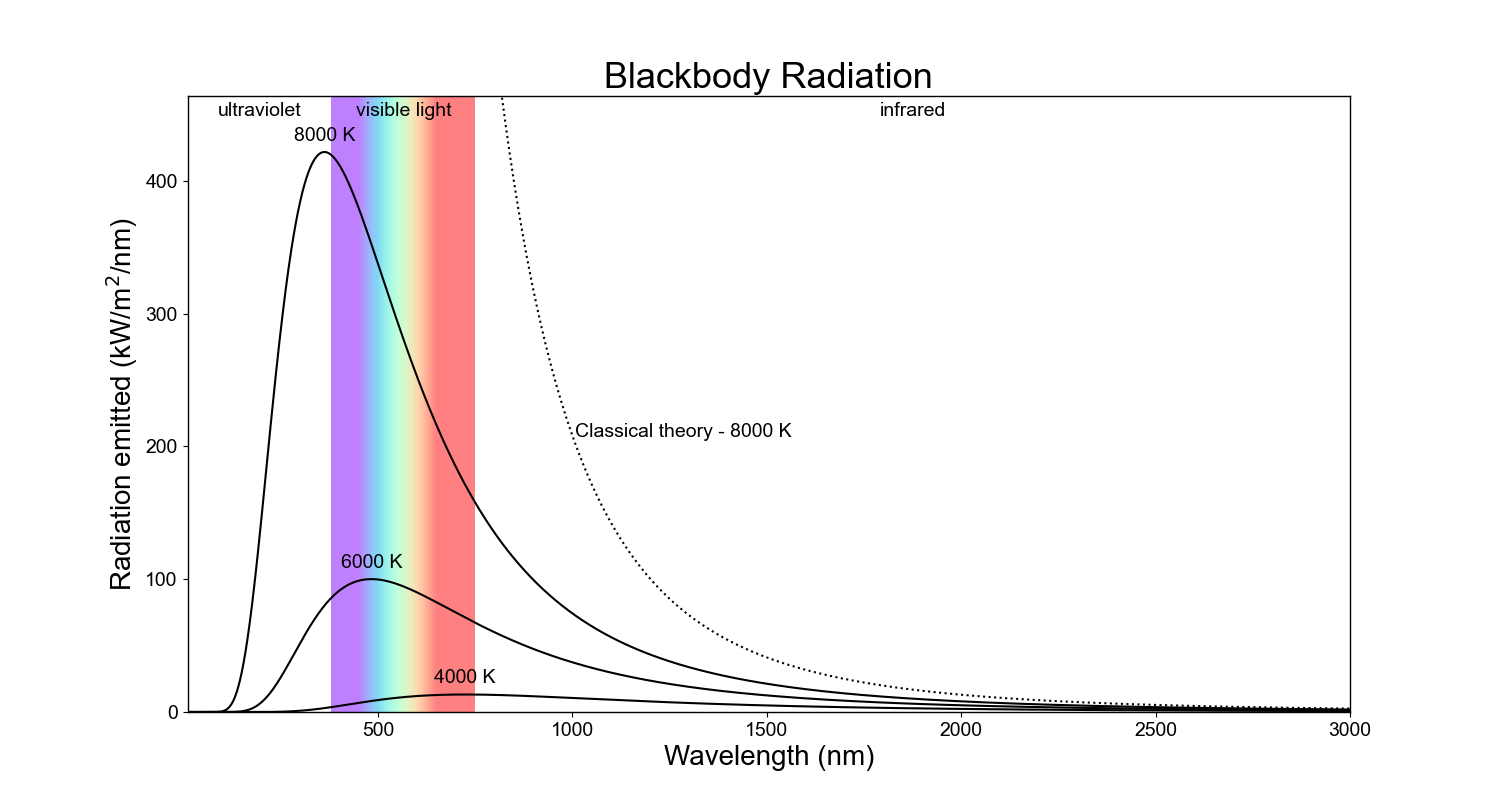
A finales del siglo XIX, la física vivía un momento de triunfo. Las leyes de Newton y Maxwell habían consolidado una visión del universo ordenado y predecible. Todo parecía estar bajo control. Sin embargo, en medio de esta calma, surgió un problema que desafiaría las bases mismas de la física clásica: la radiación del cuerpo negro.

El cuerpo negro, un objeto ideal que absorbe y emite toda la radiación incidente, presentó un comportamiento que la física clásica no podía explicar. Según la teoría clásica, a frecuencias altas, la radiación emitida debía crecer sin límite. Pero los experimentos mostraron que, en realidad, la energía disminuía en esas frecuencias. Esta contradicción, conocida como la "catástrofe ultravioleta", puso a la física contra las cuerdas y dejó claro que algo fundamental estaba fallando.

Un Hombre complejo, una Idea simple 💡

Max Planck, un físico reconocido por su rigor matemático, se propuso resolver el problema. Inicialmente, su objetivo era ajustar las teorías existentes, no revolucionarlas.

Sin embargo, lo que propuso terminó siendo mucho más audaz de lo que él mismo había anticipado.

Para resolver el problema, Planck sugirió que la energía no se emitía de forma continua, como una corriente 'continua' de agua, sino en "paquetes" o "cuantos" de energía. Entiéndase los cuantos como los "pixeles" de la luz. Esta simple pero profunda idea quedó capturada en la siguiente ecuación:

$$ E = h \nu $$

Donde:

• $E$: Es la energía del cuanto.
• $h$: Es la constante de Planck ($6.626 \times 10^{-34} , \mathrm{J \cdot s}$).
• $\nu$: Es la frecuencia de la radiación, es decir, el "color" de la luz en el caso del fotón.

Con esta fórmula, Planck logró explicar la radiación del cuerpo negro, pero también encendió la chispa de una revolución científica.

El Mundo nunca será el mismo 🌍

Albert Einstein llevó la idea de Planck más allá. Aplicó la cuantización de la energía para resolver otro misterio: el efecto fotoeléctrico. Cuando la luz golpea ciertos metales, se liberan electrones. La física clásica no podía explicar cómo ocurría esto, pero Einstein propuso que la luz estaba compuesta de partículas o "fotones", cada uno con energía $E = h \nu$.

Esta explicación no solo le valió el Premio Nobel, sino que también confirmó la noción de los cuantos ("pixeles de la realidad aparentemente continua"). Su idea demostró que la luz tenía una doble naturaleza: era a la vez partícula y onda.

El Átomo bajo revisión 🔬

Con la idea de los cuantos en el aire, Niels Bohr decidió aplicarla al modelo atómico. Sugirió que los electrones no orbitan el núcleo de forma continua, sino en órbitas discretas o "niveles energéticos". Cuando un electrón salta de una órbita a otra, emite o absorbe un fotón con x energía, explicando así las líneas espectrales de los átomos (y por derecha... el color de las cosas).

El modelo de Bohr no solo explicó cómo los átomos emiten luz en frecuencias específicas, sino que también sentó las bases para la espectroscopía moderna, una herramienta clave en la investigación científica.

El Mundo de lo Imposible 🚀

Werner Heisenberg y Erwin Schrödinger llevaron la cuántica a nuevas alturas. Heisenberg propuso el principio de incertidumbre, que afirma que

no se puede conocer con precisión la posición y el momento de una partícula al mismo tiempo.

Por otro lado, Schrödinger creó la ecuación que lleva su nombre:

$$i \hbar \frac{\partial}{\partial t} \psi(\mathbf{r}, t) = \hat{H} \psi(\mathbf{r}, t)$$

Explicación de los términos
Unidad imaginaria ($i$):
Representa el número imaginario, definido como $i = \sqrt{-1}$.

Constante de Planck reducida ($\hbar$):
Es una constante fundamental, $\hbar = \frac{h}{2\pi}$, donde $h$ es la constante de Planck.

Derivada temporal ($\frac{\partial}{\partial t}$):
Describe cómo cambia la función de onda $\psi$ con el tiempo $t$.

Función de onda ($\psi(\mathbf{r}, t)$):
Es una función que describe el estado cuántico de una partícula en términos de su posición $\mathbf{r}$ y tiempo $t$.

Operador Hamiltoniano ($\hat{H}$):
Representa la energía total del sistema, que incluye la energía cinética y la energía potencial.

Esta ecuación describe cómo evoluciona la función de onda, $\psi$, que contiene toda la información sobre el sistema cuántico. En el mundo subatómico, las partículas dejaron de comportarse como objetos clásicos y comenzaron a ser interpretadas como "ondas de probabilidad".

La función de onda se representa como $\psi(\mathbf{r}, t)$, donde $\mathbf{r}$ es la posición y $t$ es el tiempo.

El Legado Cuántico 🏛️

Lo que comenzó como un problema con la radiación del cuerpo negro se convirtió en una revolución que transformó la física y la tecnología. La mecánica cuántica explicó los átomos, los electrones y la luz de una forma que la física clásica nunca pudo.

Gracias a la mecánica cuántica, hoy tenemos láseres, semiconductores, criptografía cuántica e incluso computadoras cuánticas.

El nacimiento de la mecánica cuántica nos enseña una lección poderosa: los grandes cambios no siempre provienen de ajustes graduales, sino de actos audaces e inesperados. La catástrofe ultravioleta fue la grieta por donde se filtró una nueva forma de pensar. La cuántica no solo resolvió un problema técnico, sino que transformó para siempre la forma en que entendemos el universo.