¿Qué es un Vector? (Pista: No es una Flecha)
Antes de que podamos hablar del electrón, antes de que podamos siquiera susurrar la palabra "cuántico", necesitamos hacer algo que la mayoría de los cursos de física evitan: necesitamos ver las matemáticas.

Antes de que podamos hablar del electrón, antes de que podamos siquiera susurrar la palabra "cuántico", necesitamos hacer algo que la mayoría de los cursos de física evitan: necesitamos ver las matemáticas.
No memorizarlas. No sufrirlas. Verlas.
Y para eso, vamos a empezar con la pregunta más engañosamente simple de todas:
¿Qué es un vector?
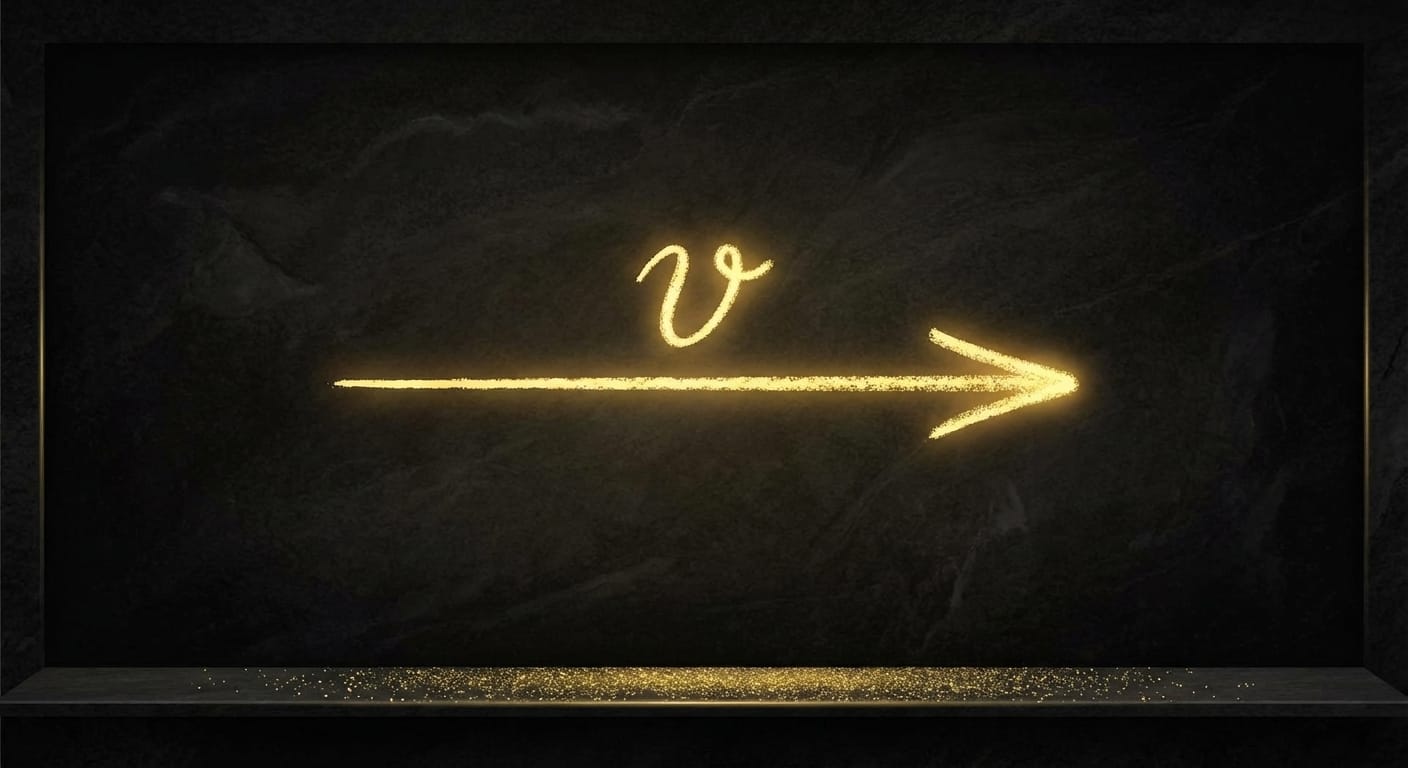
La Mentira que te Contaron en la Escuela
Si tomaste física en el bachillerato, probablemente te dijeron algo así:
"Un vector es una flecha. Tiene magnitud y dirección."
Y te mostraron una flecha apuntando hacia la derecha. Tal vez la llamaron v. Te enseñaron a sumarlas punta con cola, a multiplicarlas por números, y seguiste adelante con tu vida.
Esa definición no está mal. Pero es como decir que la música es "vibraciones en el aire". Técnicamente cierto. Profundamente incompleto.
Porque aquí está el secreto que nadie te contó:
Una canción es un vector.
Un color es un vector.
El estado de un electrón —esa cosa misteriosa que ocupa el corazón de la mecánica cuántica— es un vector.
Y ninguno de ellos es una flecha.

El Ejercicio Mental: Olvida las Flechas
Quiero que hagas algo conmigo. Cierra los ojos un momento. Bueno, no literalmente —todavía tienes que leer esto— pero quiero que sueltes la imagen de la flecha. Esa flecha roja apuntando a la derecha que vive en tu cabeza desde la secundaria. Déjala ir.
Ahora pregúntate: ¿qué hace una flecha que la hace útil?
No qué es. Qué hace.
Piensa en ello.
Una flecha te permite hacer dos cosas fundamentales:
- Puedes sumar dos flechas y obtener otra flecha. (Punta con cola, ¿recuerdas?)
- Puedes estirar o encoger una flecha multiplicándola por un número. (Duplicar su longitud, reducirla a la mitad, invertir su dirección...)
Eso es todo. Esas son las dos operaciones que definen el juego.
Ahora viene la pregunta que cambia todo:
¿Qué otras cosas en el universo permiten esas mismas dos operaciones?

Los Colores como Vectores
Imagina que tienes una pantalla de computadora frente a ti. Cada píxel de esa pantalla produce color mezclando tres luces: Roja, Verde y Azul.

Para describir cualquier color, solo necesitas tres números:
- ¿Cuánto rojo? (digamos, del 0 al 255)
- ¿Cuánto verde?
- ¿Cuánto azul?
El amarillo puro podría ser (255, 255, 0). El morado oscuro quizá (128, 0, 128).
Ahora observa esto:
¿Puedes sumar dos colores? Sí. Mezcla (100, 0, 0) con (0, 100, 0) y obtienes (100, 100, 0) —un tono de amarillo-verdoso. Dos colores combinados dan otro color.
¿Puedes escalar un color? Sí. Toma cualquier color y multiplícalo por 0.5: se vuelve más oscuro. Multiplícalo por 1.5: más brillante.
El color cumple las mismas reglas que las flechas.
El color es un vector.
No tiene dirección en el espacio físico. No apunta a ningún lado. Pero matemáticamente, se comporta exactamente igual que una flecha de tres dimensiones. Vive en un "espacio de colores" de tres dimensiones donde los ejes son Rojo, Verde y Azul.
El Sonido Estéreo como Vector
Aquí es donde la cosa se pone interesante.
Ponte unos audífonos. Hay dos parlantes: izquierdo y derecho. En cada instante, tu computadora necesita dos números para describir el sonido: qué tan fuerte suena en el oído izquierdo, y qué tan fuerte en el derecho.
Esos dos números forman un vector.

Si el sonido solo sale por la izquierda, tienes algo como (100, 0). Si solo por la derecha, (0, 100). Si está perfectamente centrado, (100, 100). Si la guitarra está un poco a la izquierda y la voz un poco a la derecha... bueno, cada una tiene su propio par de números.
¿Puedes sumar dos sonidos estéreo? Absolutamente. Lo haces cada vez que mezclas dos pistas en un programa de audio. (50, 30) + (20, 60) = (70, 90). La guitarra de la izquierda se combina con la voz de la derecha.
¿Puedes escalar un sonido estéreo? Por supuesto. Es el control de volumen. Multiplica (100, 80) por 0.5 y obtienes (50, 40) —el mismo balance espacial, pero más suave.
El sonido estéreo es un vector de dos dimensiones.
Y si tienes un sistema de sonido envolvente 5.1, cada instante de audio necesita seis números —uno por cada parlante. Eso es un vector de 6 dimensiones. Mismas reglas. Sumar. Escalar. Solo cambia el tamaño del espacio.
La Definición Real (La que Nadie te Dio)
Ahora podemos decir qué es realmente un vector:
Un vector es cualquier cosa que puedas sumar con otras de su tipo y escalar con números, siguiendo ciertas reglas sensatas.
Las "reglas sensatas" son cosas como: sumar en cualquier orden da el mismo resultado, multiplicar por 1 no cambia nada, multiplicar por 0 da el vector "vacío", etc. Son reglas que cualquier persona razonable esperaría que funcionaran.
Pero lo importante es esto: la naturaleza del objeto no importa.
Puede ser una flecha. Puede ser un color. Puede ser un sonido. Puede ser una función matemática entera. Puede ser —y aquí viene el golpe— el estado completo de una partícula subatómica.
Si cumple las reglas, es un vector.
El Espacio donde Viven los Vectores

Cada tipo de vector tiene su propio "espacio de posibilidades". Los matemáticos lo llaman espacio vectorial, pero me gusta más pensarlo como un mapa de todo lo que podría ser.
- Las flechas en una hoja de papel viven en un espacio de 2 dimensiones.
- Las flechas en el aire viven en uno de 3 dimensiones.
- Los colores RGB viven en uno de 3 dimensiones (pero diferente al espacial).
- El sonido estéreo vive en uno de 2 dimensiones (izquierda, derecha).
- El sonido envolvente 5.1 vive en uno de 6 dimensiones.
Y el estado de un electrón con espín... vive en un espacio de 2 dimensiones complejas. Pero eso viene después. Mucho después.
Por ahora, quiero que te quedes con esta imagen:
Un vector es una ubicación en un espacio de posibilidades.
No es una flecha. Es un punto en un mapa de todo lo que algo podría ser. La flecha solo representa el camino desde el origen (la "nada") hasta ese punto.
Por Qué Esto Importa para la Física Cuántica
Cuando lleguemos al corazón de la mecánica cuántica, vamos a encontrar algo extraordinario.
Un electrón, antes de que lo midas, no está en un lugar definido. No tiene una propiedad definida. Está en una superposición de todas las posibilidades.
¿Cómo describes algo así? ¿Cómo escribes matemáticamente "está un poco aquí, un poco allá, y un poco en todas partes"?
Con un vector.
Un vector que vive en un espacio de posibilidades infinitas. Un vector cuyos componentes te dicen cuánto de cada posibilidad hay en la mezcla. Un vector que no apunta a ningún lugar del espacio físico, sino que describe el estado completo de lo que algo podría ser.
La flecha de la secundaria era solo el primer paso. El entrenamiento básico. Ahora sabes que las flechas eran solo un ejemplo de algo mucho más vasto.
Los vectores son el lenguaje con el que la naturaleza describe las posibilidades.
El Experimento Mental: Tu Vector Personal
Antes de cerrar, hagamos un último ejercicio.

Imagina que tu estado emocional en este momento pudiera describirse con números. Digamos:
- Nivel de curiosidad (del 0 al 10)
- Nivel de confusión (del 0 al 10)
- Nivel de emoción por lo que viene (del 0 al 10)
Quizá ahora mismo eres algo como (7, 3, 8).
Eso es un vector. Tu estado emocional es un punto en un espacio tridimensional de posibilidades afectivas.
Y si mañana lees el siguiente capítulo y tu curiosidad aumenta, tu confusión baja, y tu emoción se mantiene... habrás viajado a otro punto en ese espacio.
Los vectores no son objetos muertos en un pizarrón.
Son la forma en que el universo describe estados, posibilidades, y transformaciones.
Y apenas estamos empezando.
Lo que Viene
En el próximo capítulo, vamos a responder una pregunta aparentemente simple:
Si tienes dos vectores, ¿cómo mides qué tan "parecidos" son?

La respuesta —el producto punto— es una de las ideas más poderosas de todas las matemáticas. Y será nuestra herramienta para calcular probabilidades en el mundo cuántico.
Pero eso es para mañana.
Por hoy, quédate con esto: un vector no es una flecha. Es una dirección en un espacio de posibilidades.

Y el espacio de posibilidades puede tener tres dimensiones, o tres millones, o infinitas.
La flecha era solo el comienzo.
"La cosa más incomprensible del universo es que sea comprensible."
— Albert Einstein
Siguiente: Capítulo 0.2 — "¿Cuánto se Parecen Dos Cosas? (El Producto Punto como Detector de Similitud)"